


Beim RSA-Algorithmus handelt es sich um das bekannteste asymmetrische Kryptoverfahren, benannt nach seinen Erfindern RIVEST-SHAMIR-ADLEMAN [RSA78, AR78].20 Die mathematische Grundlage bilden Restklassenkörper, verbunden mit der Schwierigkeit große Zahlen zu faktorisieren.
Betrachten wir in der Voraussetzung zuerst die Schlüsselerzeugung, welche im Wesen folgendermaßen abläuft:21
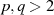 , mit
, mit 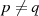 , welche das öffentliche
Modul
, welche das öffentliche
Modul 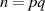 bestimmen.
bestimmen.
Zahlentheoretische Erläuterungen:
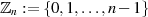 handelt es sich um einen Ring, nicht um
einen Körper.22
handelt es sich um einen Ring, nicht um
einen Körper.22
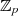 und
und 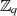 jeweils einen Primzahlenkörper.
jeweils einen Primzahlenkörper.
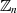 nur solche Elemente zu, die keinen gemeinsamen Teiler mit dem
Modul
nur solche Elemente zu, die keinen gemeinsamen Teiler mit dem
Modul  haben, wird ein Körper konstruierbar. Die Anzahl der Elemente
haben, wird ein Körper konstruierbar. Die Anzahl der Elemente  in
dessen multiplikativer Gruppe
in
dessen multiplikativer Gruppe 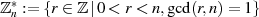 ergibt sich
mit Hilfe von EULER’s Totient-Funktion zu
ergibt sich
mit Hilfe von EULER’s Totient-Funktion zu 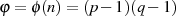 .
.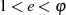 erzeugt, die keinen gemeinsamen Faktor mit
erzeugt, die keinen gemeinsamen Faktor mit 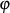 hat. Diese
(auch als öffentlicher Exponent bezeichnete) Zahl bildet die Basis des öffentlichen Schlüssels
hat. Diese
(auch als öffentlicher Exponent bezeichnete) Zahl bildet die Basis des öffentlichen Schlüssels
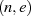 .
.
Zahlentheoretische Erläuterungen:
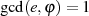 gehört
gehört  zum endlichen Körper
zum endlichen Körper 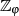 .
.
![gcd [e,(p− 1)(q− 1)]= 1](crypto184x.png) läßt sich als notwendige Voraussetzungen
läßt sich als notwendige Voraussetzungen
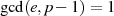 und
und 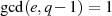 ableiten.
ableiten.
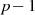 und
und 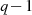 gerade Zahlen sind, muß
gerade Zahlen sind, muß  wegen des vorangegangenen
Punktes auf jeden Fall ungerade sein.
wegen des vorangegangenen
Punktes auf jeden Fall ungerade sein.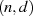 wird jetzt eine weitere Zahl
wird jetzt eine weitere Zahl 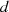 so
berechnet,23
daß
so
berechnet,23
daß 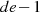 ohne Rest durch
ohne Rest durch 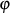 teilbar ist.
teilbar ist.
Zahlentheoretische Erläuterungen:
kann man 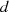 auch als Inverse des öffentlichen Exponents
auch als Inverse des öffentlichen Exponents  im Körper
im Körper 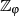 ansehen.
ansehen.
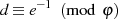
Für die Verschlüsselung wird folgende Operation auf dem Plaintext-Block  ausgeführt, wobei dieser
als Zahl
ausgeführt, wobei dieser
als Zahl 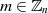 interpretiert wird:
interpretiert wird:
Die inverse Operation der Entschlüsselung wird in gleicher Art und Weise vorgenommen:
Für den Beweis 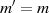 wendet man zuerst Gleichung 3.2 an und bezieht dann die Restklassendarstellung
wendet man zuerst Gleichung 3.2 an und bezieht dann die Restklassendarstellung
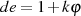 (
(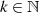 ) ein.
) ein.
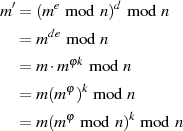
Die weitere Argumentation beruht darauf, daß 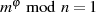 gilt und so:
gilt und so:
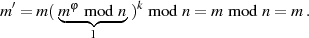
Besitzen  und
und  keinen gemeinsamen Teiler (
keinen gemeinsamen Teiler (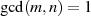 ,
, 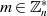 ), dann kann man auf
), dann kann man auf
 einfach EULER’s Satz (nach Formel ??) anwenden und ist fertig.
einfach EULER’s Satz (nach Formel ??) anwenden und ist fertig.
Hat  allerdings gemeinsame Teiler mit
allerdings gemeinsame Teiler mit  , dann gilt
, dann gilt 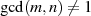 und deshalb
und deshalb 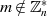 . Betrachtet
man aber die Faktorisierung von
. Betrachtet
man aber die Faktorisierung von  , dann muß
, dann muß  ein Vielfaches von
ein Vielfaches von 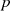 oder
oder 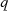 sein (wegen
sein (wegen  jedoch nicht von
jedoch nicht von 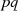 ). Unter dieser Voraussetzung wäre die Zerlegung
). Unter dieser Voraussetzung wäre die Zerlegung 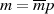 oder
oder 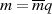 möglich, wobei jeweils
möglich, wobei jeweils 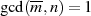 gilt. Im Fall
gilt. Im Fall 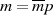 (für
(für 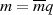 ganz genauso) läßt sich die
Modulo-Division
ganz genauso) läßt sich die
Modulo-Division  durch Kürzen von
durch Kürzen von 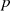 und unter Berücksichtigung von
und unter Berücksichtigung von 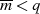 folgendermaßen vereinfachen:
folgendermaßen vereinfachen:
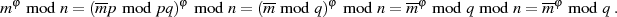
Wegen 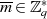 kann nun wieder der Satz von EULER zur Anwendung kommen, was den Beweis
vervollständigt.
kann nun wieder der Satz von EULER zur Anwendung kommen, was den Beweis
vervollständigt.
Eine Beschleunigung des Verfahrens läßt sich (algorithmisch) vor allem beim Entschlüsseln erzielen.24 Geht man dazu von
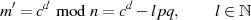
aus, dann lassen sich (durch Modulo-Division nach 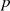 und
und 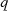 ) die folgenden zwei Kongruenzen
formulieren:
) die folgenden zwei Kongruenzen
formulieren:

Diese legen eine Anwendung des Chinesischen Restsatzes entsprechend Anhang ?? nahe [Gro00, Wel01].25

Als Voraussetzung benötigt man die Koeffizienten 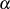 und
und 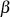 in der BéZOUT-Darstellung des größten
gemeinsamen Teilers (vgl. Formel ?? in Anhang ??)
in der BéZOUT-Darstellung des größten
gemeinsamen Teilers (vgl. Formel ?? in Anhang ??)
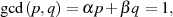
welche z. B. mit Hilfe des erweiterten euklidischen Algorithmus berechnet werden
können.26
Sie stellen, wenn man vorangegangene Gleichung nach 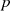 und
und 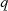 modulo-dividiert, gleichzeitig die
Inversen
modulo-dividiert, gleichzeitig die
Inversen

im Körper 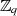 und
und 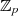 dar. Durch Anwendung des Chinesischen Restsatzes für zwei Kongruenzen
kann man nun
dar. Durch Anwendung des Chinesischen Restsatzes für zwei Kongruenzen
kann man nun 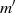 berechnen:
berechnen:
Der Vorteil liegt darin, daß die modulare Exponentiation modulo  , welche die Komplexität
, welche die Komplexität 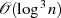 hat,27
auf zwei Operationen gleicher Art, aber mit verringerter Anzahl von Stellen verteilt.
hat,27
auf zwei Operationen gleicher Art, aber mit verringerter Anzahl von Stellen verteilt.
Die weitere Optimierung kann in drei Schritten erfolgen:

läßt sich eine lineare diophantische Gleichung ableiten (siehe auch Anhang ??):
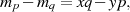
welche die Lösungsmenge
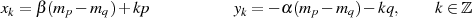
besitzt. Üblicherweise benutzt man zur Berechnung von 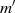 die Lösungen für
die Lösungen für 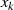 und erhält in geschlossener
Darstellung:28
und erhält in geschlossener
Darstellung:28
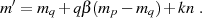
Unter der Voraussetzung 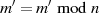 kann man vorangegangene Gleichung noch weiter
reduzieren, wenn die allgemeingültige Beziehung
kann man vorangegangene Gleichung noch weiter
reduzieren, wenn die allgemeingültige Beziehung 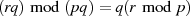 berücksichtigt
wird.
berücksichtigt
wird.
Die Vorteile dieser Darstellung liegen vor allem darin, daß
 nicht mehr nötig ist;
nicht mehr nötig ist;
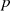 die Speicherplatzanforderungen reduziert
sind.
die Speicherplatzanforderungen reduziert
sind.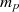 und
und 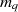 vereinfacht wird.
Eine wesentliche Zeitersparnis kommt zustande, wenn man
vereinfacht wird.
Eine wesentliche Zeitersparnis kommt zustande, wenn man  vor dessen Potenzierung in der
Länge reduziert.
vor dessen Potenzierung in der
Länge reduziert.

 , welcher ebenfalls reduziert werden
kann. Dazu muß man sich nur klarmachen, daß durch die Reduktion von
, welcher ebenfalls reduziert werden
kann. Dazu muß man sich nur klarmachen, daß durch die Reduktion von  in Punkt 2 das
Ergebnis der Potenzierung jeweils in
in Punkt 2 das
Ergebnis der Potenzierung jeweils in 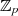 oder
oder 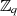 und insbesondere in der zugehörigen
multiplikativen Gruppe liegt. Da diese zyklisch ist, wiederholen sich beim Potenzieren die Werte
mit der Gruppenordnung
und insbesondere in der zugehörigen
multiplikativen Gruppe liegt. Da diese zyklisch ist, wiederholen sich beim Potenzieren die Werte
mit der Gruppenordnung 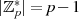 bzw.
bzw. 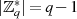 . Aus diesem Grund kann man
. Aus diesem Grund kann man 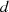 auf
die Gruppenordnung reduzieren (vgl. auch Anhang ??).
auf
die Gruppenordnung reduzieren (vgl. auch Anhang ??).

Zu der privaten Schlüsseldarstellung 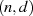 gibt es deshalb zwei Optionen:
gibt es deshalb zwei Optionen:
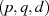 , was wegen
, was wegen 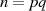 trivial erscheint;
trivial erscheint;
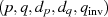 , mit
, mit 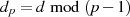 ,
,
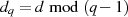 und
und 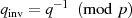 .
.Wegen der signifikanten Geschwindigkeitsvorteile wird fast immer die Quintupel-Variante verwendet [IEE00, ISO06a, PKC02].29
Um den RSA-Algorithmus praktisch auf die Verschlüsselung von Daten anzuwenden, müssen diese zuerst geeignet aufbereitet werden. Der Prozeß dieser Formatierung wird in [IEE00, PKC02] als Message Encoding Operation bezeichnet, in [PKC93a] hingegen als Encryption Block Formatting.
PKCS #1 v1.5 Mit der Methode nach [PKC93a, Kal98] gestaltet sich die Formatierung noch relativ einfach.30 Der Datenblock D wird entsprechend Abbildung 3.1 in die Struktur des sogenannten Encryption Block EB eingebunden. Auf den Encryption Block EB wird letztlich der RSA-Algorithmus nach Formel 3.2 angewendet.31
Die weiteren Elemente im Encryption Block haben folgende Bedeutung:
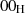 Signieren (Verwendung des privaten Schlüssels);
Signieren (Verwendung des privaten Schlüssels);
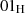 genauso wie
genauso wie 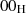 (der Unterschied liegt im Element PS);
(der Unterschied liegt im Element PS);
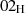 Verschlüsseln (Verwendung des öffentlichen Schlüssels).
Verschlüsseln (Verwendung des öffentlichen Schlüssels).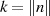 so, daß
so, daß
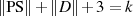 gewährleistet ist. Die Länge von PS soll mindestens 8 Byte sein, was im
Umkehrschluß die von D auf
gewährleistet ist. Die Länge von PS soll mindestens 8 Byte sein, was im
Umkehrschluß die von D auf 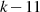 Bytes beschränkt. Das Padding selbst hängt vom Typ des
Blocks (BT) ab:
Bytes beschränkt. Das Padding selbst hängt vom Typ des
Blocks (BT) ab:
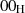 alle Bytes sind
alle Bytes sind 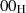 ;
;
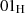 alle Bytes sind
alle Bytes sind 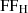 ;
;
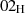 alle Bytes sind zufällig, aber ungleich
alle Bytes sind zufällig, aber ungleich 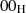 .
.Der Inhalt von PS ist beim Entschlüsseln (Byte für Byte) auf konforme Kodierung zu
prüfen [PKC93a, 9.4]. Für die Blocktypen 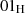 und
und 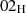 kann der Anfang (und damit auch die
Länge) des Datenblocks D ermittelt werden, indem das
kann der Anfang (und damit auch die
Länge) des Datenblocks D ermittelt werden, indem das 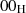 -Byte zwischen PS und D gesucht
wird. Für den Blocktyp
-Byte zwischen PS und D gesucht
wird. Für den Blocktyp 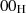 ist dieses Verfahren nur geeignet, wenn das erste Byte in D immer
ungleich
ist dieses Verfahren nur geeignet, wenn das erste Byte in D immer
ungleich 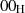 ist. Kann dies nicht vorausgesetzt werden, dann muß die Länge
ist. Kann dies nicht vorausgesetzt werden, dann muß die Länge 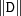 a priori bekannt
sein.32
a priori bekannt
sein.32
PKCS #1 v2.1 Nicht zuletzt wegen des sehr erfolgreiche Angriffs nach [Ble98] wird die PKCS #1 v1.5 Formatierung heute nicht mehr empfohlen. Statt dessen sollte grundsätzlich Version 2.1 nach [PKC02, JK03, IEE00, ISO06a] zum Einsatz kommen, welche Optimal Asymmetric Encryption Padding (OAEP) verwendet [BR95].33
Den Kern der Blockformatierung nach Abbildung 3.2 macht eine sogenannte Mask Generation
Function (MGF, in Abbildung 3.2 mit F bezeichnet) aus, welche selbst wiederum eine Hash-Funktion
H verwendet. Die MGF kann dasselbe leisten wie die Hash-Funktion, nämlich eine große
Eingangsmenge auf eine kleine Ausgangsmenge abbilden (mit 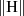 soll im folgenden die Breite eines
Hash-Wertes bezeichnet sein). Sie kann aber auch das Umgekehrte – eine kleine Eingangsmenge auf
eine größere Ausgangsmenge „zerstreuen”. PKCS #1 v2.1 legt sich zwar in der Hash-Funktion nicht
fest, definiert aber in [PKC02, B.2.1] eine konkrete Mask Generation Function, genannt
MGF1.34
soll im folgenden die Breite eines
Hash-Wertes bezeichnet sein). Sie kann aber auch das Umgekehrte – eine kleine Eingangsmenge auf
eine größere Ausgangsmenge „zerstreuen”. PKCS #1 v2.1 legt sich zwar in der Hash-Funktion nicht
fest, definiert aber in [PKC02, B.2.1] eine konkrete Mask Generation Function, genannt
MGF1.34
Die einzelnen Kodierungsschritte können folgendermaßen beschrieben werden:
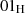 .
.
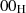 -Byte’s hinzu (Padding), so daß ein Datenblock DB der Länge
-Byte’s hinzu (Padding), so daß ein Datenblock DB der Länge 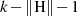 entsteht.35
entsteht.35
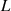 und stelle das Ergebnis als
und stelle das Ergebnis als
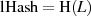 an den Anfang des Datenblocks.36
an den Anfang des Datenblocks.36
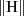 .
.
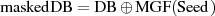 als Teil der Encoded Message (EM).
als Teil der Encoded Message (EM).
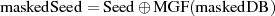 , als höherwertigen Teil von EM.
, als höherwertigen Teil von EM.
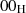 -Byte an den Anfang von EM (gewährleistet auch hier wieder
-Byte an den Anfang von EM (gewährleistet auch hier wieder
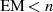 ).
).Im Gegensatz zu PKCS #1 v1.5 geht in die RSA-Verschlüsselung 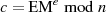 hier nun ein Wert EM ein, der keinerlei Rückschlüsse auf den Datenblock DB
zuläßt.37
hier nun ein Wert EM ein, der keinerlei Rückschlüsse auf den Datenblock DB
zuläßt.37