


Singularitäten, bei denen man von einem Pol der Ordnung  spricht (ein- oder mehrfacher Pol), sind
durch den endlichen Hauptteil
spricht (ein- oder mehrfacher Pol), sind
durch den endlichen Hauptteil
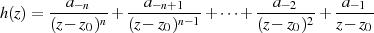
gekennzeichnet.24
Der Grund liegt in der Darstellungsmöglichkeit von 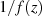 durch
durch 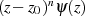 und demzufolge
und demzufolge
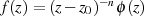 mit
mit 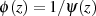 . Die Funktion
. Die Funktion 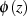 ist bei
ist bei 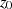 selbst analytisch,
denn alle Pole sind entsprechend ihrer Vielfachheit aus
selbst analytisch,
denn alle Pole sind entsprechend ihrer Vielfachheit aus 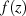 “herausgezogen” und im
Faktor
“herausgezogen” und im
Faktor 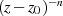 enthalten. Deshalb kann
enthalten. Deshalb kann 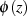 um
um 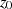 in eine Potenzreihe entwickelt
werden.25
in eine Potenzreihe entwickelt
werden.25
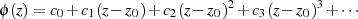
Die LAURENT-Reihe für 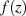 erhält dadurch die Form:
erhält dadurch die Form:
d. h. der Hauptteil 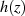 umfaßt nur eine endliche Zahl von Koeffizienten
umfaßt nur eine endliche Zahl von Koeffizienten 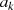 . Diese Eigenschaft
ermöglicht die Berechnung des Residuums auf der Grundlage der folgenden Formel:
. Diese Eigenschaft
ermöglicht die Berechnung des Residuums auf der Grundlage der folgenden Formel:
Die dahinter steckende Idee besteht darin, 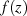 nach Gleichung 27 durch Multiplikation mit
nach Gleichung 27 durch Multiplikation mit
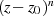 zu einer Polynomfunktion zu machen und dann den Koeffizienten
zu einer Polynomfunktion zu machen und dann den Koeffizienten  durch
durch 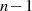 -malige
Ableitung zu extrahieren. Die Richtigkeit kann man einfach durch Einsetzen von
-malige
Ableitung zu extrahieren. Die Richtigkeit kann man einfach durch Einsetzen von 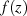 nachweisen.
nachweisen.
![---1--- d(n−1)[
resz0f(z)= (n− 1)!zli→mz0dzn−1 a−n+ a−n+1(z− z0)+ ⋅⋅⋅
n−1 n n+1 ]
+a−1(z− z0) + a0(z− z0) + a1(z− z0) + ⋅⋅⋅](analysis322x.png) |
Differentiation der einzelnen Summanden, gefolgt von der Grenzwertbildung bestätigt Beziehung 28.
![[
resz f(z)= ---1--- lim (n− 1)!a−1+ n!a0(z− z0)+ (n+-1)!a1(z− z0)2
0 (n− 1)!z→z0 1! 2!
(n+ 2)! 3 (n+ 3)! 4 ]
+ --3!---a2(z− z0) + --4!---a3(z− z0) + ⋅⋅⋅ = a− 1](analysis323x.png) |
Beispiele von Funktionen mit Pol sind 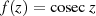 bei
bei 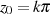 (Ordnung
(Ordnung 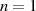 ) sowie
) sowie 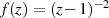 für
für 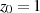 (Ordnung
(Ordnung 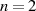 ).26
).26
Speziell für einfache Pole (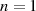 ) gilt:
) gilt: