Prev    Up    Next  

2.3 Integralformel für Ableitungen

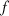Die (erste) Ableitung einer analytischen Funktion kann man auch durch ein Kurvenintegral in der komplexen Ebene ausdrücken [WW27, § 5⋅22 ]. Um dies nachzuweisen, soll zuerst CAUCHY’s Integralformel 14 in die Definition der ersten Ableitung einer Funktion f an der Stelle z (1) eingesetzt werden.

[ ] ′ f(z+-h)−-f(z) -1- 1-∮ --f(ξ)-- ∮ f(ξ)- f (z) = lih→m0 h = 2πj lhi→m0 h C ξ − z − h dξ − Cξ − zdξ

Nun werden die Argumente beider Integrale auf einen gemeinsamen Nenner gebracht, dann im Zähler ausmultipliziert und zuletzt der Grenzwert aufgelöst.15

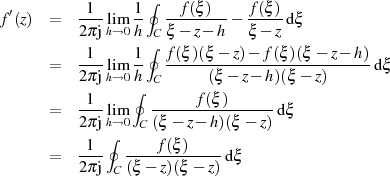
1 1∮ f(ξ) f(ξ) f′(z) = ---lim -- --------− -----dξ 2πjh→0 h∮C ξ − z− h ξ − z = -1-lim 1- f(ξ)(ξ −-z)−-f(ξ)(ξ-− z-− h-)dξ 2πjh→0 h C (ξ − z− h)(ξ − z) 1 ∮ f(ξ) = ---lim ----------------dξ 2πjh∮→0 C(ξ − z − h)(ξ − z) = -1- ----f(ξ)----dξ 2πj C (ξ − z)(ξ − z)

Der so gewonnene Ausdruck

1 ∮ f(ξ) f ′(z)= --- ------2 dξ 2πj C(ξ − z)
(15)

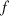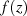ermöglicht die Berechnung der Ableitung von f an jeder Stelle z durch ein Kurvenintegral. Voraussetzung dafür ist nur, daß der Punkt z in der komplexen Ebene von einem Integrationsweg eingeschlossen wird, auf deren Rande und in dessen Inneren f(z) analytisch ist.

Durch erneute Anwendung der obigen Formeln kann man zur zweiten Ableitung 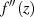f′′(z) gelangen [WW27, § 5⋅22 ].

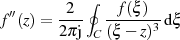
′′ 2 ∮ f(ξ) f (z)= 2πj C(ξ-−-z)3 dξ

Für weitere Ableitungen ergibt sich in der Fortsetzung die Verallgemeinerte CAUCHY’sche Integralformel

∮ f (n)(z)= n!- --f(ξ)---dξ, 2πj C (ξ − z)n+1
(16)

welche durch vollständige Induktion beweisbar ist. Sie führt zu der wesentlichen Schlußfolgerung, daß eine analytische Funktion beliebig oft differenziert werden kann.16

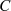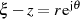Für den speziellen Fall, daß C ein Kreis mit Radius r um z ist, kann man Beziehung 16 konkretisieren. Dazu ist die Substitution ξ − z= rejθ und daraus abgeleitet 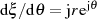dξ ∕dθ = jrejθ wieder hilfreich.

pict

In letzter Formel (18) wird die sogenannte Mittelwerteigenschaft von 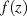f (z) bei der Integration auf dem umschließenden Kreis deutlich.