


Als ein Resultat des Satzes von CAUCHY kann man jeden Wert 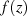 , wobei die Funktion
, wobei die Funktion 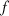 in der
Umgebung von
in der
Umgebung von  analytisch sei, durch ein Kurvenintegral ausdrücken. Dazu definiert man einfach
analytisch sei, durch ein Kurvenintegral ausdrücken. Dazu definiert man einfach
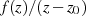 als neue Funktion, welche im Punkt
als neue Funktion, welche im Punkt 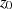 nicht analytisch ist, und integriert auf einer den
Punkt
nicht analytisch ist, und integriert auf einer den
Punkt 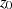 einschließenden Kurve. Da sich der Integralsatz von CAUCHY nur auf Funktionen anwenden
läßt, die im Inneren der Kurve
einschließenden Kurve. Da sich der Integralsatz von CAUCHY nur auf Funktionen anwenden
läßt, die im Inneren der Kurve 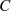 analytisch sind, umgehen wir diese Widrigkeit wie in Abbildung 1
dargestellt. Dabei wird die Kurve
analytisch sind, umgehen wir diese Widrigkeit wie in Abbildung 1
dargestellt. Dabei wird die Kurve 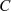 zuerst in zwei halbkreisförmige Teilkurven
zuerst in zwei halbkreisförmige Teilkurven 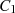 und
und 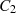 nach
Teilbild 1a zerlegt.
nach
Teilbild 1a zerlegt.
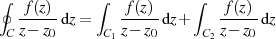
|
|
Danach werden 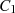 und
und 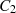 entsprechend Abbildung 1b separiert und als Kurven so geschlossen, daß
jede für sich analytisch ist. Außerdem sollen sich beide Kurven aus dem originalen Stück des
äußeren Halbkreises, bezeichnet mit
entsprechend Abbildung 1b separiert und als Kurven so geschlossen, daß
jede für sich analytisch ist. Außerdem sollen sich beide Kurven aus dem originalen Stück des
äußeren Halbkreises, bezeichnet mit 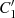 bzw.
bzw. 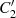 sowie dem inneren Halbkreis (inklusive
der waagerechten Teilstücke)
sowie dem inneren Halbkreis (inklusive
der waagerechten Teilstücke) 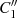 bzw.
bzw. 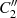 zusammensetzen. Dann gilt nach CAUCHY’s
Integralsatz 10:
zusammensetzen. Dann gilt nach CAUCHY’s
Integralsatz 10:
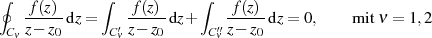
und deshalb
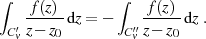
Mit der Substitution
kann man für jeden der Integralausdrücke auf den inneren Kurven
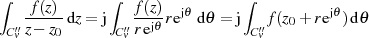
schreiben. Lassen wir jetzt den Radius  gegen Null gehen, d. h. betrachten den Wert auf
gegen Null gehen, d. h. betrachten den Wert auf 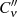 in der
Umgebung von
in der
Umgebung von 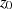 :
:
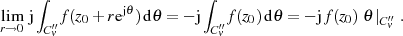
Da sich die Integrale auf dem analytischen Teil der “glattgezogenen” Kurven 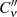 wegen der
entgegengesetzten Richtung kompensieren, ergibt sich schlußendlich:
wegen der
entgegengesetzten Richtung kompensieren, ergibt sich schlußendlich:
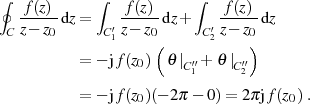
Ein ausschließlich rechnerischer Beweis ist folgendermaßen zu erbringen:
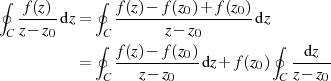
Der erste Summand stellt für 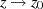 eine hebbare Singularität dar (vgl. Abschnitt 4), d. h. der
Grenzwert
eine hebbare Singularität dar (vgl. Abschnitt 4), d. h. der
Grenzwert
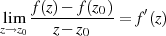
existiert. Damit ist der Integrand eine analytische Funktion für 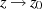 und wegen des Satzes von
CAUCHY das Integral
und wegen des Satzes von
CAUCHY das Integral
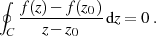
Der zweite Summand ist mit der Substitution 11
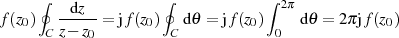 | (12) |
und somit
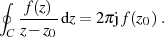 | (13) |
Benennt man noch die Variablen um (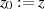 und
und 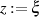 ), dann erhält man die CAUCHY’sche
Integralformel [BC03, 47].
), dann erhält man die CAUCHY’sche
Integralformel [BC03, 47].
Bei der Interpretation fällt sofort die bemerkenswerte Eigenschaft einer analytischen Funktion
(innerhalb von 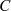 ) auf, daß der Funktionswert
) auf, daß der Funktionswert 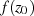 eindeutig durch die Randwerte auf der Kurve
eindeutig durch die Randwerte auf der Kurve 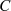 bestimmt ist.
bestimmt ist.