


Für eine analytische Funktion 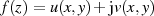 ist die Existenz einer Stammfunktion
ist die Existenz einer Stammfunktion
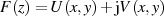 mit
mit 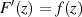 dann gegeben, wenn die Integrabilitätsbedingung nach
Gleichung 3 erfüllt und außerdem die partiellen Ableitungen stetig sind. Der erste Teil der Behauptung
ist zu verifizieren, indem man mit
dann gegeben, wenn die Integrabilitätsbedingung nach
Gleichung 3 erfüllt und außerdem die partiellen Ableitungen stetig sind. Der erste Teil der Behauptung
ist zu verifizieren, indem man mit 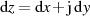 eine formale Zerlegung von
eine formale Zerlegung von 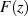 in Real- und
Imaginärteil vornimmt [WW27, §
in Real- und
Imaginärteil vornimmt [WW27, §  ].
].
Erinnern wir uns nun an die Aussage von Abschnitt 1.2, daß die Ableitung einer analytischen Funktion auch wieder analytisch ist, so gilt Gleichung 4 in der Form

und äquivalent dazu:
Mit diesen einfachen Resultaten kann man die Integranden in Formel 6 als
Differentialformen10
in 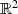 ausdrücken.
ausdrücken.
Aus der Differential- und Integralrechnung mehrerer Veränderlicher (sowie Verallgemeinerungen wie
der Vektoranalysis oder Differentialgeometrie) ist nun bekannt, daß für die totalen Differentiale  und
und 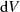 genau dann Stammfunktionen existieren, wenn
genau dann Stammfunktionen existieren, wenn  bzw.
bzw. 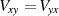 gilt. Diese
Bedingung ist für stetige Funktionen aber grundsätzlich (Satz von SCHWARZ) und für harmonische
Funktionen erst recht erfüllt.
gilt. Diese
Bedingung ist für stetige Funktionen aber grundsätzlich (Satz von SCHWARZ) und für harmonische
Funktionen erst recht erfüllt.
Nach dem Hauptsatz der Differential- und Integralrechnung existiert eine Verbindung zwischen der Stammfunktion und dem bestimmten Integral, welche unter bestimmten Bedingungen auch im komplexen Fall Gültigkeit hat [BC03, 42].
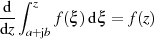
Anders als im eindimensionalen Fall muß man berücksichtigen, daß bei der Integration zwischen zwei
Punkten (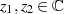 ) der Integrationsweg eine Rolle spielen kann. Ist er in Parameterform als
) der Integrationsweg eine Rolle spielen kann. Ist er in Parameterform als
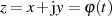 darstellbar, so gilt mit
darstellbar, so gilt mit 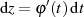 für das Kurvenintegral (zweiter Art) allgemein:
für das Kurvenintegral (zweiter Art) allgemein:
![∫ ∫
′
F(z)= Cf(z)dz= Cf [φ (t)]φ (t)dt .](analysis116x.png)
Sollte 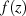 aber analytisch auf der Kurve
aber analytisch auf der Kurve 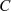 sein,11
dann ist das Integral wegunabhängig und man kann in gewohnter Art und Weise
sein,11
dann ist das Integral wegunabhängig und man kann in gewohnter Art und Weise
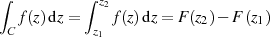 | (9) |
rechnen [BC03, 42]. Eine anschauliche Begründung steckt in den Beziehungen 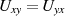 bzw.
bzw.
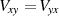 , denn sie weisen auf infinitesimaler Ebene (im Sinne des RIEMANN’schen Differentialbegriffs)
daraufhin, daß die “Fortschrittsrichtung” oder -Reihenfolge vollkommen unerheblich ist. Exakt kann die
Wegunabhängigkeit z. B. mit Hilfe der Kettenregel für Funktionen mehrerer Veränderlicher bewiesen
werden.12
Dazu gehen wir von der Parameterdarstellung
, denn sie weisen auf infinitesimaler Ebene (im Sinne des RIEMANN’schen Differentialbegriffs)
daraufhin, daß die “Fortschrittsrichtung” oder -Reihenfolge vollkommen unerheblich ist. Exakt kann die
Wegunabhängigkeit z. B. mit Hilfe der Kettenregel für Funktionen mehrerer Veränderlicher bewiesen
werden.12
Dazu gehen wir von der Parameterdarstellung 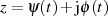 für den Integrationsweg
für den Integrationsweg 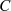 aus, bilden
in einem zweiten Schritt die Ableitungen von
aus, bilden
in einem zweiten Schritt die Ableitungen von 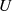 bzw.
bzw. 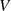 nach
nach  und ersetzen anschließend die
(entstehenden) partiellen Ableitungen durch
und ersetzen anschließend die
(entstehenden) partiellen Ableitungen durch 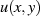 und
und  unter Zuhilfenahme von
Beziehung 7.
unter Zuhilfenahme von
Beziehung 7.
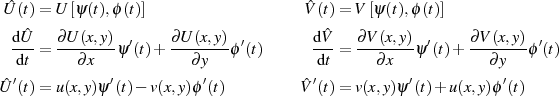
Die letzten Ausdrücke stellen genau die Differentialformen in Formel 6 dar, was uns zum Ende des Beweises bringt.
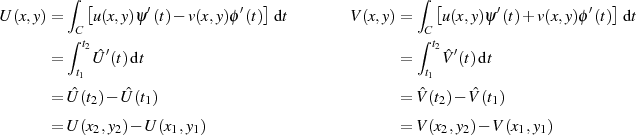
Ist die Kurve  sogar geschlossen, d. h.
sogar geschlossen, d. h.  nähert sich wieder
nähert sich wieder  , dann kommt man zum Hauptsatz
der Funktionentheorie bzw. Satz von CAUCHY [WW27, §
, dann kommt man zum Hauptsatz
der Funktionentheorie bzw. Satz von CAUCHY [WW27, §  ], [Hur00, I-5, § 6], [BC03,
44-46]:
], [Hur00, I-5, § 6], [BC03,
44-46]:
Ist 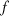 eine Funktion von
eine Funktion von  , analytisch an allen Punkten auf und innerhalb der
geschlossenen Kurve
, analytisch an allen Punkten auf und innerhalb der
geschlossenen Kurve 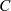 , dann gilt:13
, dann gilt:13
Sollte 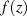 im Inneren von
im Inneren von 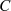 nicht überall analytisch sein, dann kann das geschlossene
Kurvenintegral einen Wert ungleich Null besitzen (siehe dazu Abschnitt 3).
nicht überall analytisch sein, dann kann das geschlossene
Kurvenintegral einen Wert ungleich Null besitzen (siehe dazu Abschnitt 3).
Damit sind uns nunmehr drei gleichwertige Kriterien für den Nachweis, daß es sich bei 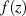 um eine
analytische Funktion handelt, bekannt:
um eine
analytische Funktion handelt, bekannt: