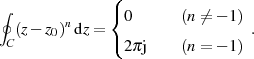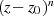
Besondere Bedeutung für viele Beweise der komplexen Analysis hat die Funktion 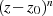 . Hier soll einmal
mit Hilfe der CAUCHY-RIEMANN’schen Differentialgleichungen deren Holomorphiegebiet bestimmt
werden.8
Wir gehen dazu von Gleichung 2 aus und bilden die partiellen Ableitungen nach
. Hier soll einmal
mit Hilfe der CAUCHY-RIEMANN’schen Differentialgleichungen deren Holomorphiegebiet bestimmt
werden.8
Wir gehen dazu von Gleichung 2 aus und bilden die partiellen Ableitungen nach  und
und 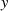 . Zur
Vereinfachung soll die Exponentialdarstellung
. Zur
Vereinfachung soll die Exponentialdarstellung 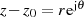 verwendet werden, wobei berücksichtigt
werden muß, daß eigentlich
verwendet werden, wobei berücksichtigt
werden muß, daß eigentlich 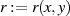 und
und 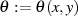 gilt.
gilt.
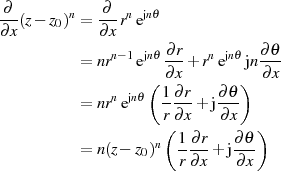
Für die Ableitung nach 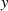 gibt es bis hierher keinen Unterschied, d. h.
gibt es bis hierher keinen Unterschied, d. h.
Setzen wir jetzt (kurz)  und erarbeiten die Zusammenhänge zwischen den Differentialen der
arithmetischen und der Exponentialform für
und erarbeiten die Zusammenhänge zwischen den Differentialen der
arithmetischen und der Exponentialform für  . Dazu soll von den bekannten
Formeln
. Dazu soll von den bekannten
Formeln

ausgegangen und dann die Ableitungen gebildet werden.

Jetzt können die so gewonnenen Ausdrücke eingesetzt werden, was mit 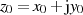 zu
zu
führt.9
Ähnlich wird mit der Ableitung nach  verfahren, nur das gedanklich noch der Zwischenschritt der
Substitution nach
verfahren, nur das gedanklich noch der Zwischenschritt der
Substitution nach  auszuführen ist.
auszuführen ist.
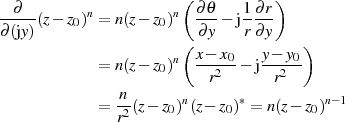
Schlußfolgerung: 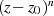 ist für positives
ist für positives  an jeder Stelle
an jeder Stelle  analytisch, denn es gilt Gleichung 2
in der Form:
analytisch, denn es gilt Gleichung 2
in der Form:
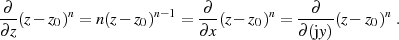
Für den Fall 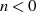 ist
ist 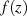 jedoch nur für
jedoch nur für 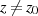 analytisch, denn beide Seiten der vorangegangenen
Äquivalenz sind sonst unbestimmt. Ein sich daraus ergebendes Resultat, welches in Abschnitt 3
bewiesen wird, ist:
analytisch, denn beide Seiten der vorangegangenen
Äquivalenz sind sonst unbestimmt. Ein sich daraus ergebendes Resultat, welches in Abschnitt 3
bewiesen wird, ist: