


Nimmt man 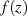 als Abbildung des Vektors
als Abbildung des Vektors 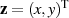 auf
auf 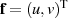 wahr, dann
ist oftmals die Funktionaldeterminante (JACOBI-Determinante) von besonderem
Interesse.6
Gerade für analytische Funktionen hat sie eine sehr einfache Lösung, welche sich ebenfalls aus den
CAUCHY-RIEMANN’schen Differentialgleichungen ableitet.
wahr, dann
ist oftmals die Funktionaldeterminante (JACOBI-Determinante) von besonderem
Interesse.6
Gerade für analytische Funktionen hat sie eine sehr einfache Lösung, welche sich ebenfalls aus den
CAUCHY-RIEMANN’schen Differentialgleichungen ableitet.
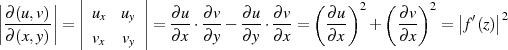
Eine Schlußfolgerung ist die, daß für alle Punkte  der komplexen Ebene, an
denen
der komplexen Ebene, an
denen 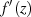 eine Wert ungleich Null hat, die Funktionaldeterminante nicht
verschwindet.7
Sollte
eine Wert ungleich Null hat, die Funktionaldeterminante nicht
verschwindet.7
Sollte 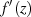 in der Umgebung von
in der Umgebung von  außerdem noch stetig sein, dann existiert eine (eindeutige)
Umkehrfunktion
außerdem noch stetig sein, dann existiert eine (eindeutige)
Umkehrfunktion 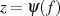 für alle
für alle 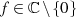 .
.