


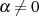
Um JORDAN’s Lemma in seiner allgemeinen Form anzuwenden, wollen wir den Prozeß jetzt etwas
umdrehen und zuerst eine komplexe Funktion 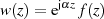 definieren. Im nächsten Schritt soll
versucht werden, das Integral
definieren. Im nächsten Schritt soll
versucht werden, das Integral 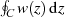 auf der geschlossenen Kurve
auf der geschlossenen Kurve 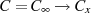 nach
Abbildung 3 für den Grenzfall
nach
Abbildung 3 für den Grenzfall  zu evaluieren.
zu evaluieren.
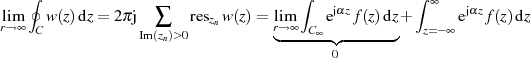
Ausgehend von dem Ergebnis
wobei 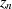 wieder die Pole (isolierte Singularitäten) der Funktion
wieder die Pole (isolierte Singularitäten) der Funktion 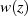 repräsentiert, kann man jetzt
noch in Gleichungen für den Real- und Imaginärteil separieren.
repräsentiert, kann man jetzt
noch in Gleichungen für den Real- und Imaginärteil separieren.
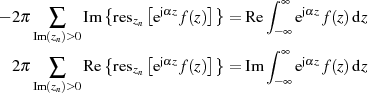
Was hier als Ergebnis präsentiert wurde, hat (insbesondere Formel 60 betreffend) besondere Bedeutung
für die inverse LAPLACE-Transformation [BC03, 81], [Sto92, 2.4.4], [Wun62, 2.22]. Unter anderem
wird für die Voraussetzung 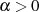 von JORDAN’s Lemma deutlich, daß sich das Konvergenzverhalten
des rechtsseitigen Integrals wegen der abgeschwächten Forderung
von JORDAN’s Lemma deutlich, daß sich das Konvergenzverhalten
des rechtsseitigen Integrals wegen der abgeschwächten Forderung 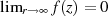 deutlich
verbessert.
deutlich
verbessert.
Die bis hierher gewonnenen Erkenntnisse bezüglich der Integration entlang der  -Achse lassen sich
auch auf den Weg entlang der
-Achse lassen sich
auch auf den Weg entlang der 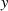 -Achse entsprechend Abbildung 5 anwenden [Wun62, 2.32]. Da nach
dem Lemma von JORDAN auch in diesem Fall das Integral auf dem Weg
-Achse entsprechend Abbildung 5 anwenden [Wun62, 2.32]. Da nach
dem Lemma von JORDAN auch in diesem Fall das Integral auf dem Weg 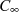 verschwindet (vgl. letzter
Absatz in Abschnitt 6, wenn
verschwindet (vgl. letzter
Absatz in Abschnitt 6, wenn 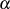 negativ-imaginär ist), wird das uneigentliche Integral mit Hilfe der
Singularitäten in der linken Halbebene berechenbar.
negativ-imaginär ist), wird das uneigentliche Integral mit Hilfe der
Singularitäten in der linken Halbebene berechenbar.
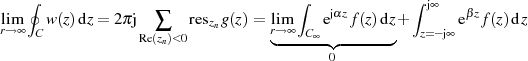
Für die Fälle von JORDAN’s Lemma mit negativem 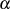 (egal ob reell oder imaginär, vgl. Abschnitt 6)
ist der entsprechende Weg
(egal ob reell oder imaginär, vgl. Abschnitt 6)
ist der entsprechende Weg 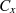 bzw.
bzw. 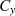 negativ anzusetzen, wenn die ganze Kurve
negativ anzusetzen, wenn die ganze Kurve 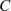 betrachtet wird.
Aus diesem Grund sind entweder die Integrationsgrenzen oder das Vorzeichen des reellen/imaginären
Integrals umzukehren.
betrachtet wird.
Aus diesem Grund sind entweder die Integrationsgrenzen oder das Vorzeichen des reellen/imaginären
Integrals umzukehren.
Tabelle 2 gibt einen Überblick, was die Berechnung uneigentlicher Integrale mit Hilfe von JORDAN’s
Lemma betrifft. Interessant ist speziell für den Fall 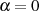 , daß es danach eine Verbindung
zwischen den Residuen der Pole in der oberen und unteren bzw. linken und rechten Halbebene
gibt:
, daß es danach eine Verbindung
zwischen den Residuen der Pole in der oberen und unteren bzw. linken und rechten Halbebene
gibt:
![∑ [resznf(z)]= − ∑ [resznf(z)] .
Im(zn)>0 Im(zn)<0](analysis656x.png)