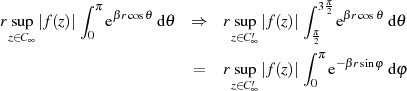Der Hilfssatz von C. JORDAN hat besondere Bedeutung bei komplexen Integralen, die teilweise im Unendlichen verlaufen. Er lautet:
Ist die Funktion 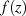 analytisch auf dem Integrationsweg
analytisch auf dem Integrationsweg 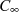 nach
Abbildung 3 (obere Halbebene) mit
nach
Abbildung 3 (obere Halbebene) mit 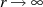 und hat für
und hat für 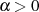 die Eigenschaft
die Eigenschaft
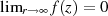 oder für
oder für 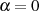 gleichwertig
gleichwertig 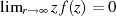 , dann gilt:
, dann gilt:
Für den Beweis gehen wir wie in [WW27, § 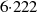 ] von
] von
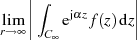 | (34) |
aus und bestimmen eine obere Schranke für den Grenzwert. Wie im ersten Punkt der Herleitung von LIOUVILLE’s Theorem gilt auch hier, daß der Betrag des Integrals kleiner als das Integral über den Betrag (des Integranden) ist.
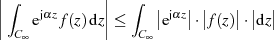
Mit der Parameterdarstellung 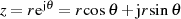 des Integrationsweges
des Integrationsweges 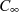 , dem
zugehörigen Differential
, dem
zugehörigen Differential 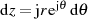 sowie der Beziehung
sowie der Beziehung 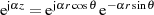 ergibt sich
schließlich
ergibt sich
schließlich
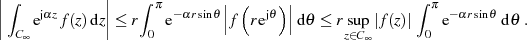 | (35) |
Der Integrand des rechtsseitigen Integrals ist bezüglich des Ordinatenwertes
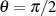 symmetrisch und kann deshalb zu
symmetrisch und kann deshalb zu 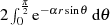 vereinfacht werden.
Weiter kann man für das Intervall
vereinfacht werden.
Weiter kann man für das Intervall 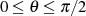 die Ungleichung
die Ungleichung 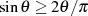 heranziehen29
und die Relation
heranziehen29
und die Relation
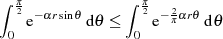 | (36) |
ableiten, welche nun bei der Berechnung des (vereinfachten) Integrals verwendet wird.
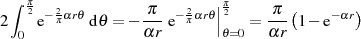 | (37) |
Einsetzen in Ungleichung 35 ergibt die Grenzwerte
was mehrere Fallunterscheidungen notwendig macht. Gemeinsam ist allen, daß es um Forderungen an
die Funktion 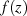 mit
mit 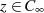 geht (d. h.
geht (d. h. 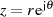 ), welche ein Verschwinden des letzten Ausdrucks
bewirken und dadurch JORDAN’s Lemma bestätigen.
), welche ein Verschwinden des letzten Ausdrucks
bewirken und dadurch JORDAN’s Lemma bestätigen.
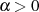 ist sofort ersichtlich, daß
ist sofort ersichtlich, daß 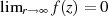 gelten
muß. Außerdem ist erwähnenswert, daß Ungleichung 39 die bekannte Abschätzung
gelten
muß. Außerdem ist erwähnenswert, daß Ungleichung 39 die bekannte Abschätzung
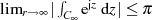 beinhaltet, welche sich für
beinhaltet, welche sich für 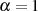 und
und 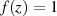 ergibt.
ergibt.
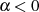 führen zu folgenden Veränderungen an den bisherigen Formeln:
führen zu folgenden Veränderungen an den bisherigen Formeln:
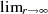 für Beziehung 37, dann ist das Ergebnis
für Beziehung 37, dann ist das Ergebnis 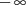 .
.
Aus diesem Dilemma kann man sich jedoch durch Drehung des Integrationsweges in die
negativ-imaginäre Halbebene (angedeutet in Abbildung 3) befreien. Mit den Grenzen
![[π,2π ]](analysis431x.png) und der Substitution
und der Substitution 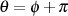 ist man in der Lage, den Ausgangspunkt
nach Ungleichung 35 wiederherzustellen und die Beweisschritte vom Fall
ist man in der Lage, den Ausgangspunkt
nach Ungleichung 35 wiederherzustellen und die Beweisschritte vom Fall 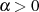 zu
übernehmen.30
zu
übernehmen.30
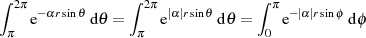
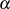 jedoch Null sein, dann verschwindet der Nenner auf der
rechten Seite von Ungleichung 39 und man muß (schärfer noch)
jedoch Null sein, dann verschwindet der Nenner auf der
rechten Seite von Ungleichung 39 und man muß (schärfer noch) 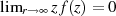 fordern. JORDAN’s Lemma 33 nimmt unter genannten Voraussetzungen die spezielle
Form
fordern. JORDAN’s Lemma 33 nimmt unter genannten Voraussetzungen die spezielle
Form
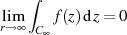 | (40) |
an.
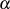 zu, dann geht mit
zu, dann geht mit
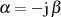 der Betrag des Integrals nach Formel 34 in
der Betrag des Integrals nach Formel 34 in
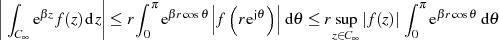
über. Wegen des Cosinus-Terms im Exponenten wird JORDAN’s Lemma hier nicht
zutreffen, was aber (wieder) durch Veränderung des Integrationsweges behoben
werden kann. Dazu wählt man als Integrationsgrenzen ![[π∕2,3π ∕2]](analysis442x.png) und substituiert
und substituiert
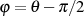 bzw.
bzw. 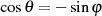 . Durch den neuen Integrationsweg
. Durch den neuen Integrationsweg 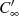 im
Unendlichen (vgl. auch Abbildung 5) wird die ursprüngliche Form von Ungleichung 35
wieder hergestellt, womit der Beweis auf dem gewohnten Weg fortgesetzt werden
kann.31
im
Unendlichen (vgl. auch Abbildung 5) wird die ursprüngliche Form von Ungleichung 35
wieder hergestellt, womit der Beweis auf dem gewohnten Weg fortgesetzt werden
kann.31