


LIOUVILLE’s Satz soll hier, etwas anders als z. B. in [WW27, §  ], in drei Schritten hergeleitet
werden.
], in drei Schritten hergeleitet
werden.
 angeben kann. Dazu gehen wir davon aus, daß
angeben kann. Dazu gehen wir davon aus, daß
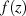 auf dem Integrationsweg
auf dem Integrationsweg 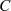 analytisch und mit
analytisch und mit 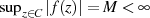 beschränkt
ist. Liegen also auf
beschränkt
ist. Liegen also auf 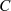 keine Singularitäten, dann gilt folgende Ungleichung [BC03, 37]:
keine Singularitäten, dann gilt folgende Ungleichung [BC03, 37]:
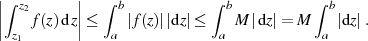
Geht man der
besseren Vorstellung halber von einem Integrationsweg in Parameterdarstellung aus, d. h.
 und
und  , dann ist
, dann ist
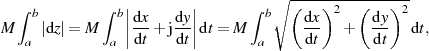
wobei letzter Ausdruck genau die Bogenlänge 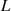 der Kurve
der Kurve  darstellt. Ist
darstellt. Ist 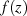 wie
vorausgesetzt auf dem gesamten Integrationsweg analytisch und beschränkt, dann gilt für den
Betragswert des Integrals [WW27, §
wie
vorausgesetzt auf dem gesamten Integrationsweg analytisch und beschränkt, dann gilt für den
Betragswert des Integrals [WW27, §  ], [BC03, 41]:
], [BC03, 41]:
 ten Ableitung von
ten Ableitung von  an der Stelle
an der Stelle 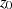 von Interesse [WW27, §
von Interesse [WW27, §  ]. Wir gehen dabei von Beziehung 17, also einem kreisförmigen
Integrationsweg mit Radius
]. Wir gehen dabei von Beziehung 17, also einem kreisförmigen
Integrationsweg mit Radius  um
um 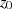 , aus um deren Wert (bzw. obere Grenze) zu
bestimmen.
, aus um deren Wert (bzw. obere Grenze) zu
bestimmen.

Anwendung von Ungleichung 31 führt mit der Länge 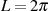 und der Abkürzung
und der Abkürzung
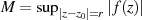 zu
zu
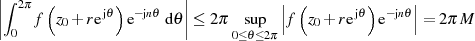
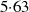 ]
folgendermaßen lautet:
]
folgendermaßen lautet:
Sei 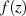 analytisch und beschränkt mit
analytisch und beschränkt mit 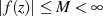 für alle
für alle  (sogar
für
(sogar
für 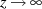 , also eine ganze Funktion), dann ist
, also eine ganze Funktion), dann ist 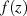 eine Konstante.
eine Konstante.
Der Beweis steckt in Ungleichung 32, denn dort heißt es für 
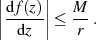
Läßt man nun  gehen um die gesamte komplexe Ebene einzuschließen, so gilt (unter der
wesentlichen Voraussetzung, daß
gehen um die gesamte komplexe Ebene einzuschließen, so gilt (unter der
wesentlichen Voraussetzung, daß  überall beschränkt sei):
überall beschränkt sei):
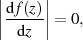
d. h. 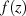 ist konstant.
ist konstant.
Interessant ist im Umkehrschluß, daß jede nicht-konstante analytische Funktion Singularitäten besitzen muß. Ansonsten wäre sie entweder nicht beschränkt oder nicht analytisch, würde also die Voraussetzungen nicht erfüllen.
Noch zwei Bemerkungen zum Satz von LIOUVILLE, die seine Bedeutung unterstreichen sollen:
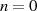 das sogenannte Maximumprinzip nach [Cau54,
II-6]:
das sogenannte Maximumprinzip nach [Cau54,
II-6]:
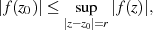
d. h. der Betrag des Funktionswertes im Punkt 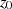 ist immer kleiner oder gleich dem
größten Betragswert von
ist immer kleiner oder gleich dem
größten Betragswert von 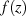 auf dem Kreis mit (irgendeinem) Radius
auf dem Kreis mit (irgendeinem) Radius  um
um 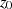 .
.
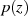 mit komplexen
Koeffizienten mindestens eine Nullstelle in
mit komplexen
Koeffizienten mindestens eine Nullstelle in 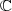 haben muß, ist mit seiner Hilfe sehr elegant
möglich. Denn hätte die Funktion
haben muß, ist mit seiner Hilfe sehr elegant
möglich. Denn hätte die Funktion 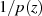 nirgendwo einen Pol (auf
nirgendwo einen Pol (auf  uneingeschränkt
analytisch), dann wäre sie überall beschränkt. Nach LIOUVILLE müßte es sich bei
uneingeschränkt
analytisch), dann wäre sie überall beschränkt. Nach LIOUVILLE müßte es sich bei 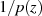 also um eine Konstante handeln, was der Voraussetzung widerspricht, daß
also um eine Konstante handeln, was der Voraussetzung widerspricht, daß 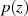 ein
nicht-konstantes Polynom ist [FB00, II-3].
ein
nicht-konstantes Polynom ist [FB00, II-3].