Der Residuensatz ist eine logische Fortführung bzw. Anwendung der Erkenntnisse des
vorigen Abschnittes, in welchem der Begriff des Residuums erstmalig auftauchte [FB00,
III-6]. Er ermöglicht die einfache Berechnung von (geschlossenen) Kurvenintegralen,
wenn innerhalb des Integrationsweges ein oder mehrere Singularitäten von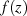 
liegen.20
Einleitend müssen wir uns aber mit der Frage befassen, wie sich der Einschluß mehrerer
singulärer Punkte auf den Wert des umlaufenden Integrals auswirkt. Dazu soll im Beispiel nach
Abbildung 2a um zwei solcher Punkte auf dem (geschlossenen) Weg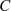 
integriert werden [Mar95,
10.3].
Ist die Funktion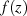 
außer an den Singularitäten und insbesondere auf 
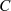analytisch, dann kann man den Integrationsweg entsprechend Abbildung 2b
verändern.21
Eine solche Wahl des Integrationsweges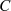 
führt dazu, daß sich die Kurvenintegrale über 
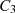und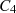 
aufheben, also
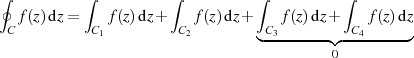
gilt. Dieser Umstand ist graphisch in Abbildung 2c dargestellt und kann folgendermaßen zusammengefaßt werden:
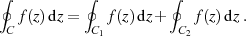
Umschließt ein Kurvenintegral auf seinem Weg 
Singularitäten, dann kann
dessen Wert durch separate Integration um alle 
singulären Punkte bestimmt
werden.22
![∮ [∮ ]
f(z)dz= ∑ f(z)dz
C n Cn](analysis275x.png) | (24) |
Entwickelt man jetzt die Funktion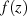 
um die einzelnen Singularitäten herum zu einzelnen
LAURENT-Reihen, so kann man mit Hilfe von Gleichung 21 den Residuensatz formulieren.
Wie berechnet man jedoch das Residuum an einem (isolierten) singulären Punkt ohne Kenntnis der
LAURENT-Reihenentwicklung vo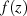n 
? Zur Beantwortung dieser Frage betrachten wir (die) drei
Typen von Singularitäten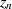 
, welche sich durch die Art des Hauptteils 
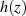der LAURENT-Reihe von
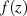unterscheiden [FB00, III-4.10].
